1. A binary classifier¶
In this tutorial we train and test a binary-quantum-classifier.
1.1. Dataset generation¶
We generate a dataset and its labels using numpy and we randomly split
it in a train and test with train_test_split
from sklearn.
import numpy as np
np.random.seed(42)
n_pc = 100 # Points per component
# Create a matrix on the point and its symmetry
px, py = 0.75, 0.75
X = np.asarray(n_pc * [[px, py]] +
n_pc * [[-px, -py]]
)
# Add gaussian noise
X += 0.7 * np.random.randn(*X.shape)
# Create target vecor
y = np.concatenate((np.zeros(n_pc), np.ones(n_pc)))
# Split in train and test
from sklearn.model_selection import train_test_split
input_train, input_test, target_train, target_test =\
train_test_split(X, y, test_size=.3)
1.2. Circuit definition¶
Now, we need to define the structure of the circuit, we do this using a
make_circuit function.
This function can have any name, but must take exactly three arguments, in the
following order: (bdr, x, params).
These correspond to a circuitBuilder, to an input vector, and to a
parameter vector.
def simple_circuit(bdr, x, params):
bdr.allin(x).cz(0,1).allin(params[:2])
bdr.cz(0,1).allin(params[2:4])
return bdr
This corresponds to the circuit in the following figure, where we use input
gates and CZ entanglements.
The precise syntax of make_circuit and the meaning of the gates are explained in the “Defining a quantum circuit” tutorial .
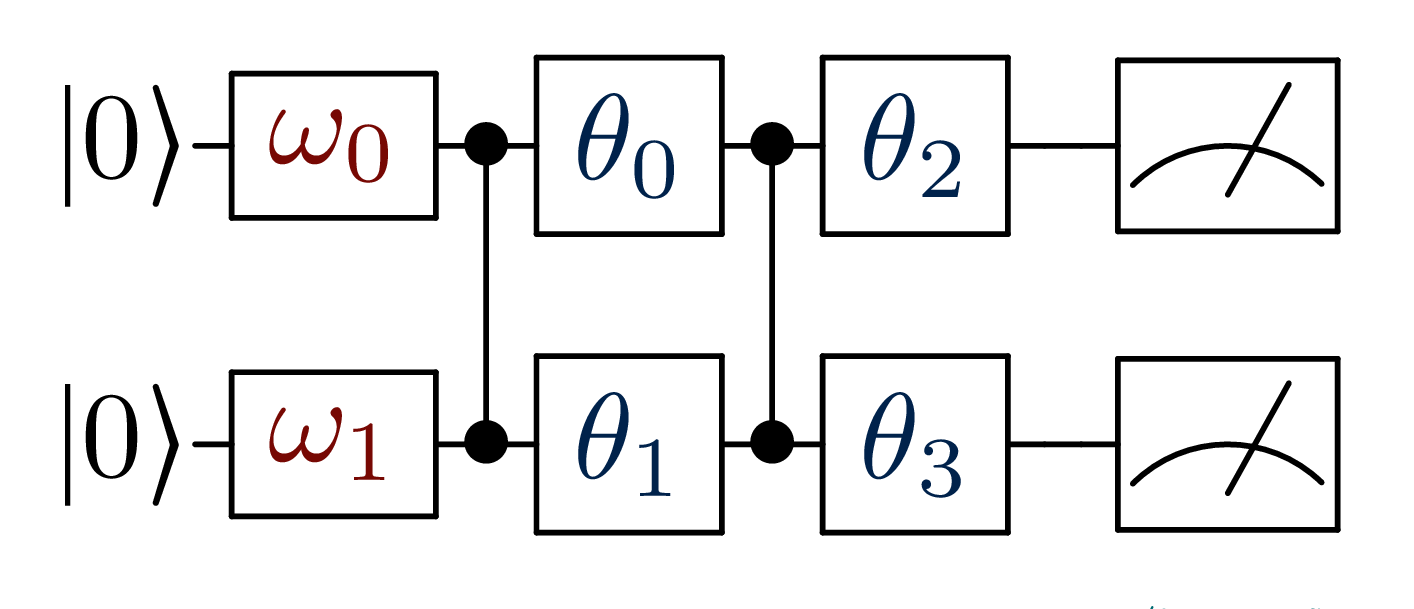
Now, we need to translate our description in a runnable circuit.
This is obtained using a circuitML class, which interacts with a backend;
in this case we use The manyq simulator.
from polyadicqml.manyq import mqCircuitML
qc = mqCircuitML(make_circuit=simple_circuit,
nbqbits=2, nbparams=4)
1.3. Model training¶
At this point, we are ready to create and train our first quantum Classifier.
We only need to choose which bitsrings will be used to predict the classes.
from polyadicqml import Classifier
# Choose two bitstrings
bitstr = ["01", "10"]
model = Classifier(qc, bitstr).fit(input_train, target_train)
1.4. Predict on new data¶
Once the model is trained, we can easily predict the class of any new sample.
pred_train = model(input_train)
pred_test = model(input_test)
And we can assert the performance of the model by confronting the predictions and the true labels.
>>> from polyadicqml.utility import print_results
>>> print_results(target_train, pred_train, name="train")
##########################
Confusion matrix on train:
[[66 3]
[ 4 67]]
Accuracy : 0.95
>>> print_results(target_test, pred_test, name="test")
##########################
Confusion matrix on test:
[[30 1]
[ 2 27]]
Accuracy : 0.95
1.5. Source code¶
This example script can be found in the GitHub example page as
quickstart.py.