2. A Gaussian XOR problem¶
Our second example is the XOR problem. We place four points over the cartesian axes so to create a centered square; the two points on x-axis are labeled as 1, while those on y-axis as 0.
2.1. Dataset generation¶
We use numpy to generate a dataset of 200 points by sampling 50 points from 4 gaussian distibutions centered at the said points. The label of each sample is given by the center of its distribution.
import numpy as np
n_pc = 50 # Number of points per cluster
# Create a matrix of vertices of the centered square
X = np.asarray(n_pc * [[1.5, 0.]] +
n_pc * [[-1.5, 0.]] +
n_pc * [[0., -1.5]] +
n_pc * [[0., 1.5]]
)
# Add gaussian noise
X += .5 * np.random.randn(*X.shape)
# Create target vecor
y = np.concatenate((np.zeros(2*n_pc), np.ones(2*n_pc)))
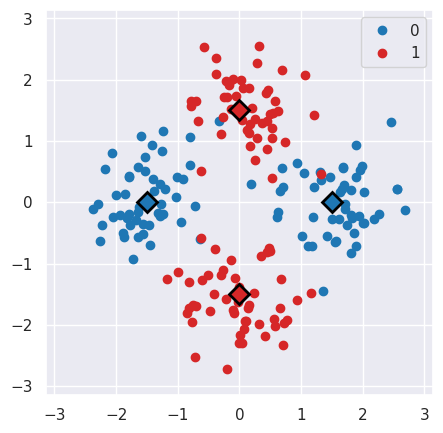
This generates the following dataset, where the circles represent the samples and the squares the distribution centers.
2.2. Circuit definition¶
Now, we define the circuit structure using the make_circuit function.
def make_circuit(bdr, x, params):
"""Generate the circuit corresponding to input `x` and `params`.
Parameters
----------
bdr : circuitBuilder
A circuit builder.
x : vector-like
Input sample
params : vector-like
Parameter vector.
Returns
-------
circuitBuilder
Instructed builder
"""
bdr.allin(x[[0,1]])
bdr.cz(0, 1).allin(params[[0,1]])
bdr.cz(0, 1).allin(params[[2,3]])
return bdr
2.3. Model training¶
Finally, we can create and train the classifier.
We instantiate the circuitML subclass that we prefer, in this case the one using the fast manyq simualtor, specifying the number of qubits and of parameters.
from polyadicqml.manyq import mqCircuitML
nbqbits = 2
nbparams = 6
qc = mqCircuitML(make_circuit=make_circuit,
nbqbits=nbqbits, nbparams=nbparams)
Then, we create and train the quantum classifer, specifying on which bitstrings we want to read the predicted classes.
from polyadicqml import Classifier
bitstr = ['00', '01']
model = Classifier(qc, bitstr)
model.fit(X, y)
2.4. Predict on new data¶
We can use a model to predict on some new datapoints X_test that it
never saw before.
To obtain the bitstring probabilities, we can just call the model:
pred_prob = model.predict_proba(X_test)
Then, we can retrieve the label of each point as the argmax of the corresponding probabilities. Otherwise, we can combine the two operations by using the shorthand:
y_pred = model(X_test)
For instance, going back to our XOR problem, we can predict the label of
each point on a grid that covers , to
assess the model accuracy.
Using some list comprehension, it would look like this:
t = np.linspace(-np.pi,np.pi, num = 50)
X_test = np.array([[t1, t2] for t1 in t for t2 in t])
y_pred = model(X_test)
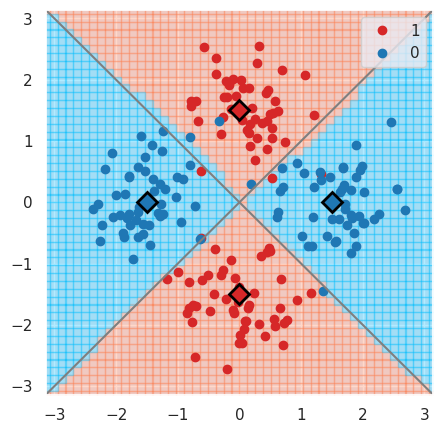
We can now plot the predictions and see that the model is very close to the bayesian prediction (whose decision boundaries are shown as grey lines), which is the best possible.
2.5. Source code¶
The example script, producing the plots, can be found in the GitHub example
page as example-XOR.py.