3. The Iris Flower dataset¶
For this use case, we perform ternary classification on the Iris Flower dataset. In this case, we will train the model using a simulator and then test it on a real quantum computer, using IBMQ access.
3.1. Data preparation¶
We load the dataset from scikit-learn and we split it in a train and a test set, representing respectively 60% and 40% of the samples.
from sklearn import datasets
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
data = iris.data
target = iris.target
# Train-test split
input_train, input_test, target_train, target_test =\
train_test_split(data, target, test_size=.4, train_size=.6, stratify=target)
Then, we center it and rescale it so that it has zero mean and all the
feature values fall between . (Actually, with
our scaling, last interval should cover 99% of a gaussian with the same
mean and std; it covers all points on almost all splits.)
import numpy as np
# NORMALIZATION
mean = input_train.mean(axis=0)
std = input_train.std(axis=0)
input_train = (input_train - mean) / std / 3 * 0.95 * np.pi
input_test = (input_test - mean) / std / 3 * 0.95 * np.pi
3.2. Circuit definition¶
Now, we define a circuit on two qubits, again using the make_circuit syntax.
Thanks to the functional nature, we can use other fuctions to group
repeated instructions.
def block(bdr, x, p):
bdr.allin(x[[0,1]])
bdr.cz(0,1).allin(p[[0,1]])
bdr.cz(0,1).allin(x[[2,3]])
bdr.cz(0,1).allin(p[[2,3]])
def irisCircuit(bdr, x, params):
# The fist block uses all `x`, but
# only the first 4 elements of `params`
block(bdr, x, params[:4])
# Add one entanglement not to have two adjacent input
bdr.cz(0,1)
# The block repeats with the other parameters
block(bdr, x, params[4:])
return bdr
Which corresponds to the following circuit:
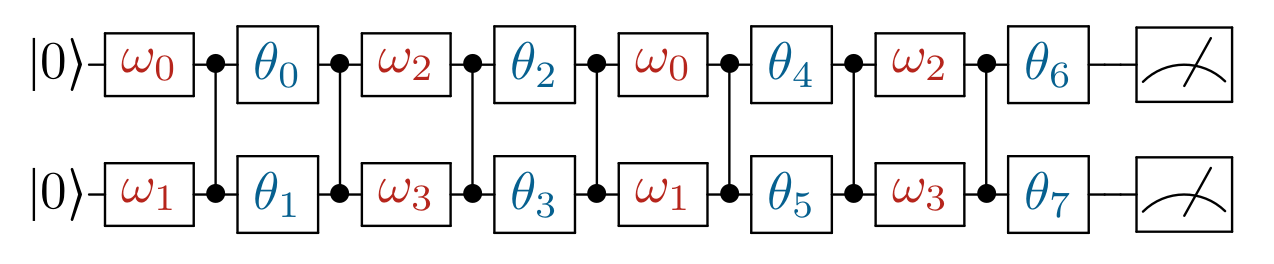
3.3. Model training¶
As in the previous use case, we need a circuitML and a classifier, which we train with the corresponding dataset.
from polyadicqml.manyq import mqCircuitML
from polyadicqml import Classifier
nbqbits = 2
nbparams = 8
qc = mqCircuitML(make_circuit=irisCircuit,
nbqbits=nbqbits, nbparams=nbparams)
bitstr = ['00', '01', '10']
model = Classifier(qc, bitstr).fit(input_train, target_train)
We can print the training scores.
>>> from polyadicqml.utility import print_results
>>> pred_train = model(input_train)
>>> print_results(target_train, pred_train, name="train")
Confusion matrix on train:
[[30 0 0]
[ 0 30 0]
[ 0 4 26]]
Accuracy : 0.9556
3.4. Model Testing¶
Once the model is trained, we can test it.
Furthermore, we can keep the trained parameters and change the circuit
backend, as long as the make_circuit function is the same.
So, if we have an IBMQ account configured and access to a quantum
backend (in this case ibmq-burlington), we can run the test on an actual hardware.
Note
To access IBM Quantum systems, you need to configure your IBM Quantum account. Detailed instructions are provided on the Qiskit installation guide. You can verify your setup if the following runs without producing errors:
>>> from qiskit import IBMQ
>>> IBMQ.load_account()
If you do not have an IBM Quantum account, you can still use Qiskit Aer simulators.
We use the Backends utility class, along with the qkCircuitML, which
implements circuitML for qiksit use.
NOTE that we must provide a number of shots, as the backend is not a
simulator; the job size is inferred if left empty, but we chose to set it at 40.
from polyadicqml.qiskit.utility import Backends
from polyadicqml.qiskit import qkCircuitML
backend = Backends("ibmq_burlington", hub="ibm-q")
qc = qkCircuitML(backend=backend,
make_circuit=irisCircuit,
nbqbits=nbqbits, nbparams=nbparams)
model.set_circuit(qc)
model.nbshots = 300
model.job_size = 40
pred_test = model(input_test)
Finally, we can print the test scores:
>>> from polyadicqml.utility import print_results
>>> pred_test = model(input_test)
>>> print_results(target_test, pred_test, name="test")
Confusion matrix on test:
[[20 0 0]
[ 0 20 0]
[ 0 0 20]]
Accuracy : 1.0
3.5. Source code¶
The example script, producing the plots, can be found in the GitHub example
page as example-iris.py.